Contoh:
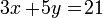 → persamaan dengan dua variabel x dan y.
→ persamaan dengan dua variabel x dan y.
 → persamaan dengan dua variabel α dan β.
→ persamaan dengan dua variabel α dan β.
Penyelesaian PLDV
Eliminasi
Eliminasi adalah menghilangkan salah satu variabel.Contoh:
Carilah nilai Δ dan t dari persamaan berikut dengan cara eliminasi.
4Δ + 3t = 34 | X1 → 4Δ + 3t = 34
5Δ + t = 37 | X3 → 15Δ + 3t = 111
______________ -
-11Δ = -77
Δ = 7
Setelah kita mendapatkan nilai Δ yaitu 7, kita akan mencari nilai t.Untuk mencari nilai t, persamaan nomor 1 dikalikan dengan 5 dan persamaan nomor 2 dikalikan dengan 4. Kedua persamaan dikurangi agar variabel Δ hilang.
4Δ + 3t = 34 | X5 → 20Δ + 15t = 170
5Δ + t = 37 | X4 → 20Δ + 4t = 148
______________ -
11t = 22
t = 2
Jadi Δ = 7 dan t = 2.Substitusi
Substitusi adalah menggantikan salah satu variabel ke persamaan yang lain.Contoh:
Carilah nilai e dan f dari persamaan tersebut dengan metode substitusi.
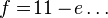
Masukkan persamaan berikut hingga menjadi:
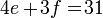
4e + 3(11 - e) = 31
4e + 33 - 3e = 31
e = 31 - 33
e = -2
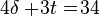

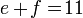
Tidak ada komentar:
Posting Komentar